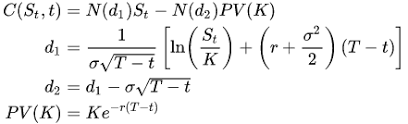How Option Traders Can Determine the Right Price for Calls and Puts
The Black-Scholes option pricing model may be the most used and best known theoretical option pricing model among several developed in recent decades. In simplest terms, it is a mathematical formula intended to determine the price of an option (or warrant) relative to multiple inputs, like a stock’s price, or volatility, or the risk-free interest rate. Said another way, it’s a tool that tells traders if an option is overvalued or undervalued at its current price.
The model is named after its creators, Fisher Black and Myron Scholes. The duo unveiled the formula and premise in their 1973 paper ‘The Pricing of Options and Corporate Liabilities.’ Since then, it has become the preferred pricing model within the option trading world, even with its flaws.
Multiple Variables in the Black-Scholes Model
The popularity of the Black-Scholes pricing model is largely the result of its completeness. Though other models exist – and are still in use – few have successfully incorporated the underlying stock’s current price, the option’s strike price, length of time until the option expires, an estimate of future volatility (or implied volatility), and risk free rate of return. The way those five pieces of data are incorporated becomes clear in the model’s formula:
C = S N(d1) – X e-rT N(d2)
where
- C = price of the call option
- S = price of the underlying stock
- X = option exercise price
- r = risk-free interest rate
- T = current time until expiration
- N() = area under the normal curve
- d1 = [ ln(S/X) + (r + σ2/2) T ] / σ T1/2
- d2 = d1 – σ T1/2
Criticisms of the Black-Scholes Option Pricing Model
Like all theoretical models, the Black-Scholes option pricing model isn’t perfect. Critics are quick to point out six specific shortcomings of the formula:
- One of the inputs – a stock’s volatility – is sometimes arbitrarily determined
- It can overvalue deep out-of-the-money calls, yet undervalue deep in-the-money calls.
- It assumes the risk-free rate and the stock’s volatility are constant.
- It assumes stock prices are continuous and involatile
- It assumes a stock pays no dividends
- It assumes the option will not be exercised until expiration day
Though the concerns about the model’s accuracy are justifiable, adjustments can be made to the model’s theoretical prices to account for such things as dividends and pre-expiration exercise. So, the drawbacks of the theory/formula are generally dismissible.
It should also be noted that several variations of the formula have been developed. Each offers its own advantages and disadvantages, yet each is also a derivation of the original Black-Scholes formula.
Option Trading With the Black-Scholes Model
It’s not necessary for a trader to learn the pricing formula above to successfully trade options. In fact, many traders may be using the model without even knowing it – most option calculators are designed to price options according the Black-Scholes methodology. The key is to understand that the model is simply an odds-making tool.